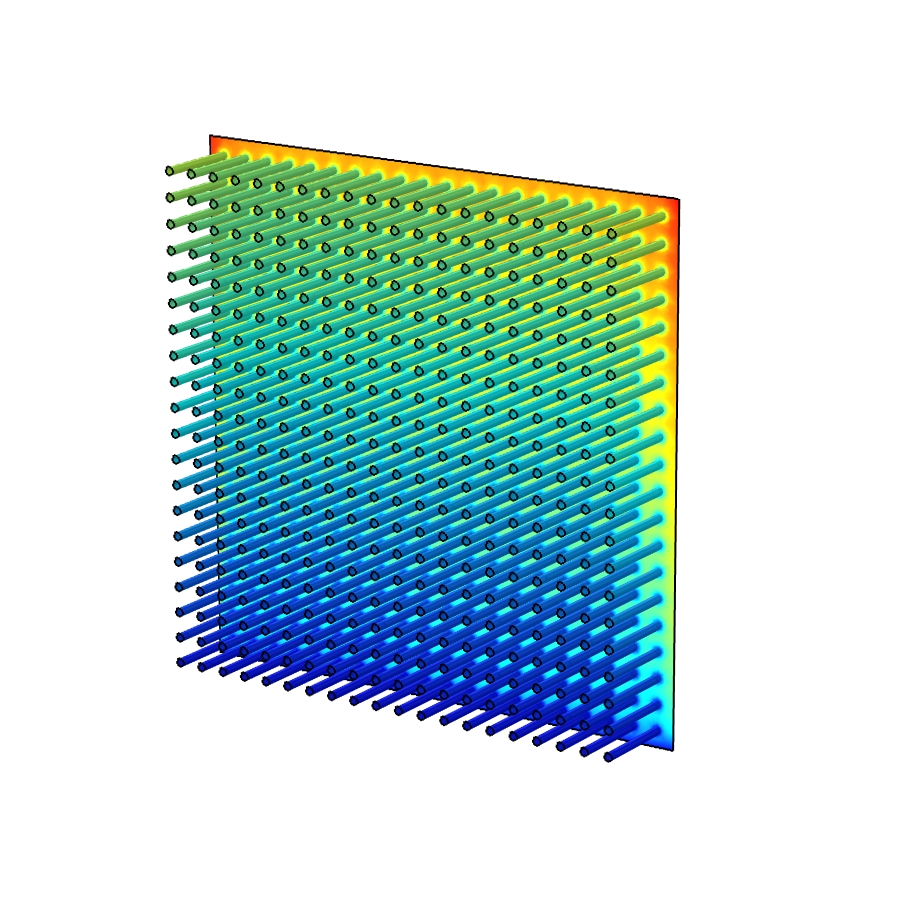
Saving Time and Money for Rockwell Automation
Problem: As Rockwell Automation looked to improve product functionality, engineers relied on developing physical prototypes to test heat sink designs for its powerful microprocessor chips. This approach left mechanical engineers scrambling at the end of the design cycle to find an electronics cooling solution that would fit the prototypes and not delay new product releases. […]
Saving Time and Money for Rockwell Automation Read More »